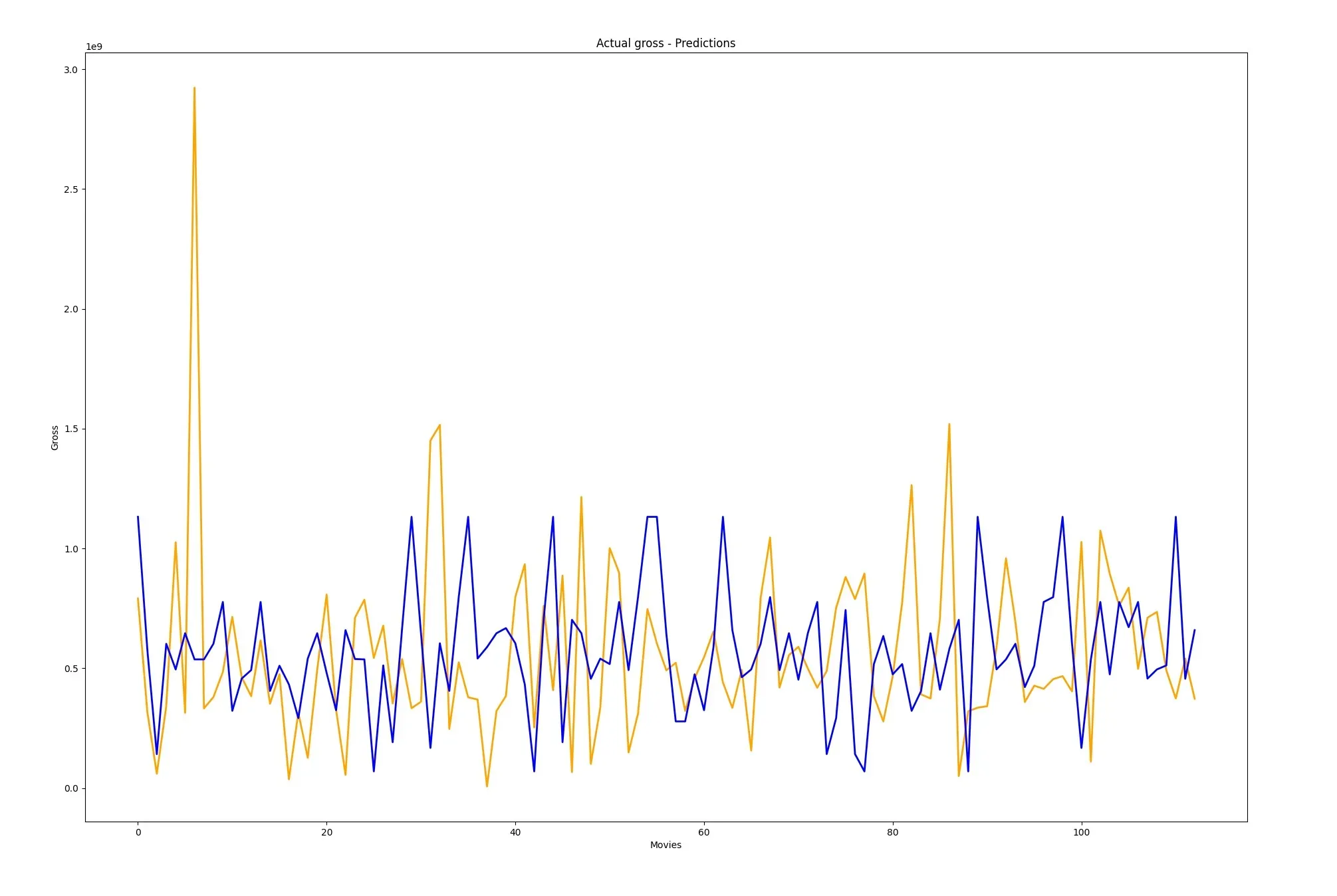
What is Mean Absolute Error (MAE)
Mean Absolute Error (MAE) is a popular loss function for evaluating the performance of regression models. In other words, it measures the average difference between predicted and actual values.
Furthermore, we’ll dive into how to interpret it, and why it’s essential in machine learning models. So let’s get started!
How to Calculate Mean Absolute Error?
Calculating MAE is pretty straightforward. To clarify, you subtract each predicted value from the corresponding actual value, take the sum of the absolute values of these differences, and then compute the mean.
This results in a single number that represents the average error of your model’s predictions.
Following formula expresses the process we just described above.
Interpreting Mean Absolute Error: What is a Good Value?
When interpreting MAE, a lower value is generally better. To explain, a low MAE indicates that your model’s predictions are closer to the actual values.
However, the acceptable range for MAE depends on the problem you’re trying to solve and the scale of your data.
Using MAE to Evaluate Model Performance
To understand the performance of your model, you can compare the MAE to other metrics, such as Mean Squared Error (MSE) or Mean Absolute Percentage Error (MAPE).
Each metric offers different insights:
- MAE vs. MSE: While MAE measures the average absolute difference, MSE squares the differences before averaging them. This means that MSE is more sensitive to large errors, while MAE treats all errors equally.
- MAE vs. MAPE: MAPE is similar to MAE but calculates the percentage error instead of the absolute error. This makes it more suitable for comparing the performance of models on datasets with different scales.
Conclusion
To conclude, understanding and interpreting error metrics like MAE is crucial for evaluating the performance of your machine learning models.
Furthermore, by comparing MAE to other metrics, you can gain insights into how well your model is performing and make informed decisions about model selection and improvement.